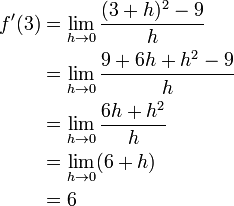PEMROGRAMAN LINIER
(Sumber : Siringoringo, 2005)

Pemrograman Linier disingkat PL merupakan metode matematik dalam mengalokasikan sumber daya yang terbatas untuk mencapai suatu tujuan seperti memaksimumkan keuntungan dan meminimumkan biaya. PL banyak diterapkan dalam masalah ekonomi, industri, militer, social dan lain-lain. PL berkaitan dengan penjelasan suatu kasus dalam dunia nyata sebagai suatu model matematik yang terdiri dari sebuah fungsi tujuan linier dengan beberapa kendala linier.
Karakteristik Pemrograman Linier
Sifat linearitas suatu kasus dapat ditentukan dengan menggunakan beberapa cara. Secara statistik, kita dapat memeriksa kelinearan menggunakan grafik (diagram pencar) ataupun menggunakan uji hipotesa. Secara teknis, linearitas ditunjukkan oleh adanya sifat proporsionalitas, additivitas, divisibilitas dan kepastian fungsi tujuan dan pembatas.
Sifat proporsional dipenuhi jika kontribusi setiap variabel pada fungsi tujuan atau penggunaan sumber daya yang membatasi proporsional terhadap level nilai variabel. Jika harga per unit produk misalnya adalah sama berapapun jumlah yang dibeli, maka sifat proporsional dipenuhi. Atau dengan kata lain, jika pembelian dalam jumlah besar mendapatkan diskon, maka sifat proporsional tidak dipenuhi. Jika penggunaan sumber daya per unitnya tergantung dari jumlah yang diproduksi, maka sifat proporsionalitas tidak dipenuhi.
Sifat additivitas mengasumsikan bahwa tidak ada bentuk perkalian silang diantara berbagai aktivitas, sehingga tidak akan ditemukan bentuk perkalian silang pada model. Sifat additivitas berlaku baik bagi fungsi tujuan maupun pembatas (kendala). Sifat additivitas dipenuhi jika fungsi tujuan merupakan penambahan langsung kontribusi masing-masing variabel keputusan. Untuk fungsi kendala, sifat additivitas dipenuhi jika nilai kanan merupakan total penggunaaan masing-masing variabel keputusan. Jika dua variabel keputusan misalnya merepresentasikan dua produk substitusi, dimana peningkatan volume penjualan salah satu produk akan mengurangi volume penjualan produk lainnya dalam pasar yang sama, maka sifat additivitas tidak terpenuhi.
Sifat divisibilitas berarti unit aktivitas dapat dibagi ke dalam sembarang level fraksional, sehingga nilai variabel keputusan non integer dimungkinkan.
Sifat kepastian menunjukkan bahwa semua parameter model berupa konstanta. Artinya koefisien fungsi tujuan maupun fungsi pembatas merupakan suatu nilai pasti, bukan merupakan nilai dengan peluang tertentu.
Keempat asumsi (sifat) ini dalam dunia nyata tidak selalu dapat dipenuhi. Untuk meyakinkan dipenuhinya keempat asumsi ini, dalam pemrograman linier diperlukan analisis sensitivitas terhadap solusi optimal yang diperoleh.
Formulasi Permasalahan
Urutan pertama dalam penyelesaian adalah mempelajari sistem relevan dan mengembangkan pernyataan permasalahan yang dipertimbangakan dengan jelas. Penggambaran sistem dalam pernyataan ini termasuk pernyataan tujuan, sumber daya yang membatasi, alternatif keputusan yang mungkin (kegiatan atau aktivitas), batasan waktu pengambilan keputusan, hubungan antara bagian yang dipelajari dan bagian lain dalam perusahaan, dan lain-lain.
Penetapan tujuan yang tepat merupakan aspek yang sangat penting dalam formulasi masalah. Untuk membentuk tujuan optimalisasi, diperlukan identifikasi anggota manajemen yang benar-benar akan melakukan pengambilan keputusan dan mendiskusikan pemikiran mereka tentang tujuan yang ingin dicapai.
Pembentukan model matematik
Tahap berikutnya yang harus dilakukan setelah memahami permasalahan optimasi adalah membuat model yang sesuai untuk analisis. Pendekatan konvensional riset operasional untuk pemodelan adalah membangun model matematik yang menggambarkan inti permasalahan. Kasus dari bentuk cerita diterjemahkan ke model matematik. Model matematik merupakan representasi kuantitatif tujuan dan sumber daya yang membatasi sebagai fungsi variabel keputusan. Model matematika permasalahan optimal terdiri dari dua bagian. Bagian pertama memodelkan tujuan optimasi. Model matematik tujuan selalu menggunakan bentuk persamaan. Bentuk persamaan digunakan karena kita ingin mendapatkan solusi optimum pada satu titik. Fungsi tujuan yang akan dioptimalkan hanya satu. Bukan berarti bahwa permasalahan optimasi hanya dihadapkan pada satu tujuan. Tujuan dari suatu usaha bisa lebih dari satu. Tetapi pada bagian ini kita hanya akan tertarik dengan permasalahan optimal dengan satu tujuan.
Bagian kedua merupakan model matematik yang merepresentasikan sumber daya yang membatasi. Fungsi pembatas bisa berbentuk persamaan (=) atau pertidaksamaan (≤ atau ≥). Fungsi pembatas disebut juga sebagai konstrain. Konstanta (baik sebagai koefisien maupun nilai kanan) dalam fungsi pembatas maupun pada tujuan dikatakan sebagai parameter model. Model matematika mempunyai beberapa keuntungan dibandingakan pendeskripsian permasalahan secara verbal. Salah satu keuntungan yang paling jelas adala model matematik menggambarkan permasalahan secara lebih ringkas. Hal ini cenderung membuat struktur keseluruhan permasalahan lebih mudah dipahami, dan membantu mengungkapkan relasi sebab akibat penting. Model matematik juga memfasilitasi yang berhubungan dengan permasalahan dan keseluruhannya dan mempertimbangkan semua keterhubungannya secara simultan. Terakhir, model matematik membentuk jembatan ke penggunaan teknik matematik dan komputer kemampuan tinggi untuk menganalisis permasalahan.
Di sisi lain, model matematik mempunyai kelemahan. Tidak semua karakteristik sistem dapat dengan mudah dimodelkan menggunakan fungsi matematik. Meskipun dapat dimodelkan dengan fungsi matematik, kadang-kadang penyelesaiannya sulit diperoleh karena kompleksitas fungsi dan teknik yang dibutuhkan.
Bentuk umum pemrograman linier adalah sebagai berikut :
Fungsi tujuan :
Maksimumkan atau minimumkan z = c1x1 + c2x2 + ... + cnxn
Sumber daya yang membatasi :
a11x1 + a12x2 + ... + a1nxn = /≤ / ≥ b1
a21x1 + a22x2 + … + a2nxn = /≤ / ≥ b2
…
am1x1 + am2x2 + … + amnxn = /≤ / ≥ bm
x1, x2, …, xn ≥ 0
Simbol x1, x2, ..., xn (xi) menunjukkan variabel keputusan. Jumlah variabel keputusan (xi) oleh karenanya tergantung dari jumlah kegiatan atau aktivitas yang dilakukan untuk mencapai tujuan. Simbol c1,c2,...,cn merupakan kontribusi masing-masing variabel keputusan terhadap tujuan, disebut juga koefisien fungsi tujuan pada model matematiknya.Simbol a11, ...,a1n,...,amn merupakan penggunaan per unit variabel keputusan akan sumber daya yang membatasi, atau disebut juga sebagai koefisien fungsi kendala pada model matematiknya. Simbol b1,b2,...,bm menunjukkan jumlah masing-masing sumber daya yang ada. Jumlah fungsi kendala akan tergantung dari banyaknya sumber daya yang terbatas.
Pertidaksamaan terakhir (x1, x2, …, xn ≥ 0) menunjukkan batasan non negatif. Membuat model matematik dari suatu permasalahan bukan hanya menuntut kemampuan matematik tapi juga menuntut seni permodelan. Menggunakan seni akan membuat permodelan lebih mudah dan menarik.
Kasus pemrograman linier sangat beragam. Dalam setiap kasus, hal yang penting adalah memahami setiap kasus dan memahami konsep permodelannya. Meskipun fungsi tujuan misalnya hanya mempunyai kemungkinan bentuk maksimisasi atau minimisasi, keputusan untuk memilih salah satunya bukan pekerjaan mudah. Tujuan pada suatu kasus bisa menjadi batasan pada kasus yang lain. Harus hati-hati dalam menentukan tujuan, koefisien fungsi tujuan, batasan dan koefisien pada fungsi pembatas.
Contoh Kasus yang diselesaikan
Pada sub bab ini terdapat 10 kasus dengan karakteristik berbeda yang sudah diselesaikan untuk memperkaya pembaca dalam ilmu dan seni permodelan. Pahami dan perhatikan teknik permodelannya dengan hati-hati.
- Seorang pengrajin menghasilkan satu tipe meja dan satu tipe kursi. Proses yang dikerjakan hanya merakit meja dan kursi. Dibutuhkan waktu 2 jam untuk merakit 1 unit meja dan 30 menit untuk merakit 1 unit kursi. Perakitan dilakukan oleh 4 orang karyawan dengan waktu kerja 8 jam perhari. Pelanggan pada umumnya membeli paling banyak 4 kursi untuk 1 meja. Oleh karena itu pengrajin harus memproduksi kursi paling banyak empat kali jumlah meja. Harga jual per unit meja adalah Rp 1,2 juta dan per unit kursi adalah Rp 500 ribu.
Formulasikan kasus tersebut ke dalam model matematiknya !
Solusi :
Hal pertama yang harus dilakukan adalah mengidentifikasi tujuan, alternatif keputusan dan sumber daya yang membatasi. Berdasarkan informasi yang diberikan pada soal, tujuan yang ingin dicapai adalah memaksimumkan pendapatan. Alternatif keputusan adalah jumlah meja dan kursi yang akan diproduksi. Sumber daya yang membatasi adalah waktu kerja karyawan dan perbandingan jumlah kursi dan meja yang harus diproduksi (pangsa pasar ).
Langkah berikutnya adalah memeriksa sifat proporsionalitas, additivitas, divisibilitas dan kepastian. Informasi di atas tidak menunjukkan adanya pemberian diskon, sehingga harga jual per meja maupun kursi akan sama meskipun jumlah yang dibeli semakin banyak. Hal ini mengisyaratkan bahwa total pendapatan yang diperoleh pengrajin proposional terhadap jumlah produk yang terjual. Penggunaan sumber daya yang membatasi , dalam hal ini waktu kerja karyawan dan pangsa pasar juga proporsional terhadap jumlah meja dan kursi yang diproduksi. Dengan demikian dapat dinyatakan sifat proporsionalitas dipenuhi. Total pendapatan pengrajin merupakan jumlah pendapatan dari keseluruhan meja dan kursi yang terjual. Penggunaan sumber daya ( waktu kerja karyawan dan pangsa pasar) merupakan penjumlahan waktu yang digunakan untuk memproduksi meja dan kursi. Maka dapat dinyatakan juga sifat additivitas dipenuhi. Sifat divisibilitas dan kepastian juga dipenuhi.
Ada dua variabel keputusan dan dua sumber daya yang membatasi. Fungsi tujuan meru[pakan maksimisasi, karena semakin besar pendapatan akan semakin disukai oleh pengrajin. Fungsi kendala pertama (batasan waktu) menggunakan pertidaksamaan ≤, karena waktu yang tersedia dapat digunakan sepenuhnya atau tidak, tapi tidak mungkin melebihi waktu yang ada. Fungsi kendala yang kedua bisa menggunakan ≤ atau ≥ tergantung dari pendefinisianvariabelnya.
Kita definisikan :
x1 = jumlah meja yang akan diproduksi
x2 = jumlah kursi yang akan diproduksi
Model umum Pemrograman Linier kasus di atas adalah :
Fungsi tujuan :
Maksimumkan z = 1.2 x1 + 0.5 x2
Kendala :
2x1 + 0.5 x2 ≤ 32
x1/x2 ≥ ¼ atau 4x1≥ x2 atau 4x1 – x2 ≥ 0
x1 , x2 ≥ 0
- Seorang peternak memiliki 200 kambing yang mengkonsumsi 90 kg pakan khusus setiap harinya. Pakan tersebut disiapkan menggunakan campuran jagung dan bungkil kedelai dengan komposisi sebagai berikut :
Bahan | Kg per kg bahan |
Kalsium | Protein | Serat | Biaya (Rp/kg) |
Jagung | 0.001 | 0.09 | 0.02 | 2000 |
Bungkil kedelai | 0.002 | 0.60 | 0.06 | 5500 |
Kebutuhan pakan kambing setiap harinya adalah paling banyak 1% kalsium, paling sedikit 30% protein dan paling banyak 5% serat.
Formulasikan permasalahan di atas kedalam model matematiknya !
Solusi :
Hal pertama yang harus dilakukan adalah mengidentifikasi tujuan , alternative keputusan dan sumber daya yang membatasi. Berdasarkan informasi yang diberikan pada soal, tujuan yang ingin dicapai adalah meminimumkan biaya pembelian bahan pakan. Alternative keputusan adalah jumlah jagung dan bungkil kedelai yang akan digunakan. Sumber daya yang membatasi adalah kandungan kalsium, protein dan serat pada jagung dan bungkil kedelai, serta kebutuhan jumlah pakan per hari.
Langkah berikutnya adalah memeriksa sifat proporsionalitas, additivitas, divisibilitas dan kepastian. Informasi di atas tidak menunjukkan adanya pemberian diskon, sehingga harga pembelian jagung dan bungkil kedelai per kg tidak berbeda meskipun pembelian dalam jumlah besar. Hal ini mengisyaratkan bahwa total biaya yang harus dikeluarkan peternak proporsional terhadap jumlah jagung dan bungkil kedelai yang dibeli. Penggunaan sumber daya yang membatasi, dalam hal ini komposisi jagung dan bungkil kedelai akan serat, protein dan kalsium proporsional terhadap jumlah jagung dan bungkil. Dengan demikian dapat dinyatakan sifat proporsionalitas dipenuhi. Total pengeluaran pembelian bahan pakan merupakan penjumlahan pengeluaran untuk jagung dan bungkil kedelai. Jumlah masing-masing serat, protein dan kalsium yang ada di pakan khusus merupakan penjumlah serat, protein dan kalsium yang ada pada jagung dan bungkil kedelai. Jumlah pakan khusus yang dihasilkan merupakan penjumlahan jagung dan bungkil kedelai yang digunakan. Dengan demikian sifat additivitas dipenuhi. Sifat divisibilitas dan kepastian juga dipenuhi.
Ada dua variabel keputusan dan empat sumber daya yang membatasi. Fungsi tujuan merupakan minimisasi, karena semakin kecil biaya akan semakin disukai oleh peternak. Fungsi kendala pertama (batasan jumlah pakan yang dibutuhkan per hari) menggunakan persamaan (=), fungsi kendala kedua (kebutuhan kalsium) dan kendala keempat (kebutuhan serat) menggunakan pertidaksamaan ≤, dan fungsi kendala ketiga (kebutuhan akan protein) menggunakan pertidaksamaan ≥.
Kita definisikan :
x1 = jumlah jagung yang akan digunakan
x2 = jumlah bungkil kedelai yang akan digunakan
Model umum Pemrograman linier kasus di atas oleh karenanya adalah :
Fungsi tujuan : minimumkan z = 2000 x1 + 5500 x2
Kendala :
x1 + x2 = 90
0.001 x1 + 0.002 x2 ≤ 0.9
0.09 x1 + 0.6 x2 ≥ 27
0.02 x1 + 0.06 x2 ≤ 4.5
x1, x2 ≥ 0
3. Suatu bank kecil mengalokasikan dana maksimum Rp 180 juta untuk pinjaman pribadi dan pembelian mobil satu bulan kedepan. Bank mengenakan biaya suku bunga per tahun 14% untuk pinjaman pribadi dan 12% untuk pinjaman pembelian mobil. Kedua tipe pinjaman itu dikembalikan bersama dengan bunganya satu tahun kemudian. Jumlah pinjaman pembelian mobil paling tidak dua kali lipat dibandingkan pinjaman pribadi. Pengalaman sebelumnya menunjukkan bahwa 1% pinjaman pribadi merupakan kredit macet.
Formulasikan masalah di atas kedalam bentuk model matematiknya !
Solusi :
Hal pertama yang harus dilakukan adalah mengidentifikasi tujuan, alternatif keputusan dan sumber daya yang membatasi. Berdasarkan informasi yang diberikan pada soal, tujuan yang ingin dicapai adalah memaksimumkan pendapatan bunga dan pengembalian pinjaman. Alternatif keputusan adalah jumlah alokasi pinjaman pribadi dan pinjaman mobil. Sumber daya yang membatasi adalah jumlah alokasi anggaran untuk kredit bulan depan dan perbandingan antara jumlah kredit pribadi dan pembelian mobil.
Sifat proporsionalitas, additivitas, divisibilitas dan kepastian dipenuhi.
Ada dua variabel keputusan yaitu jumlah anggaran untuk pinjaman pribadi dan pinjaman pembelian mobil, dan dua sumber daya yang membatasi. Fungsi tujuan merupakan maksimisasi , karena semakin besar pendapatan akan semakin disukai oleh manajemen bank.
Kita definisikan :
x1 = jumlah anggaran untuk pinjaman pribadi
x2 = jumlah anggaran untuk pinjaman pembelian mobil.
Model umum Pemrograman Linier kasus diatas adalah :
Fungsi tujuan : Maksimumkan z = (0.14 – 0.01) x1 + 0.12 x2
Kendala :
x1 + x2 ≤ 180
x2 ≥ 2x1 atau -2x1 + x2 ≥ 0
x1, x2 ≥ 0
4. Suatu pabrik perakitan radio menghasilkan dua tipe radio, yaitu HiFi-1 dan HiFi-2 pada fasilitas perakitan yang sama. Lini perakitan terdiri dari 3 stasiun kerja. Waktu perakitan masing-masing tipe pada masing-masing stasiun kerja adalah sebagai berikut :
Stasiun kerja | Waktu perakitan per unit (menit) |
HiFi-1 | HiFi-2 |
1 | 6 | 4 |
2 | 5 | 5 |
3 | 4 | 6 |
Waktu kerja masing-masing stasiun kerja adalah 8 jam per hari. Masing-masing stasiun kerja membutuhkan perawatan harian selama 10%, 14% dan 12% dari total waktu kerja (8 jam) secara berturut-turut untuk stasiun kerja 1,2 dan 3.
Formulasikan permasalahan ini kedalam model matematiknya !
Solusi :
Alternatif keputusan adalah : radio tipe HiFi-1 (x1) dan radio tipe HiFi-2 (x2).
Tujuannya adalah memaksimumkan jumlah radio HiFi-1 dan HiFi-2 yang diproduksi.
Sumber daya pembatas adalah : jam kerja masing-masing stasiun kerja dikurangi dengan waktu yang dibutuhkan untuk perawatan.
Waktu produktif masing-masing stasiun kerja oleh karenanya adalah :
Stasiun 1 : 480 menit – 48 menit = 432 menit
Stasiun 2 : 480 menit – 67.2 menit = 412.8 menit
Stasiun 3 : 480 menit – 57.6 menit = 422.4 menit.
Model umum pemrograman linier :
Maksimumkan z = x1 + x2
Kendala :
6x1 + 4x2 ≤ 432
5x1 + 5x2 ≤ 412.8
4x1 + 6x2 ≤ 422.4
x1, x2 ≥ 0
5. Dua produk dihasilkan menggunakan tiga mesin. Waktu masing-masing mesin yang digunakan untuk menghasilkan kedua produk dibatasi hanya 10 jam per hari. Waktu produksi dan keuntungan per unit masing-masing produk ditunjukkan table di bawah ini :
Produk | Waktu produksi (menit) |
Mesin 1 | Mesin 2 | Mesin 3 | Mesin 4 |
1 | 10 | 6 | 8 | 2 |
2 | 5 | 20 | 15 | 3 |
Formulasikan permasalahan di atas ke dalam model matematiknya !
Solusi :
Alternatif keputusan adalah : produk 1 (x1) dan produk 2 (x2).
Tujuannya adalah memaksimumkan keuntungan
Sumber daya pembatas adalah : jam kerja masing-masing mesin.
Model umum pemrograman linier :
Maksimumkan z = 2x1 + 3x2
Kendala :
10 x1 + 5 x2 ≤ 600
6 x1 + 20 x2 ≤ 600
8 x1 + 15 x2 ≤ 600
x1, x2 ≥ 0
6. Empat produk diproses secara berurutan pada 2 mesin. Waktu pemrosesan dalam jam per unit produk pada kedua mesin ditunjukkan table di bawah ini :
Mesin | Waktu per unit (jam) |
Produk 1 | Produk 2 | Produk 3 | Produk 4 |
1 | 2 | 3 | 4 | 2 |
2 | 3 | 2 | 1 | 2 |
Biaya total untuk memproduksi setiap unit produk didasarkan secara langsung pada jam mesin. Asumsikan biaya operasional per jam mesin 1 dan 2 secara berturut-turut adalah $10 dan $5. Waktu yang disediakan untuk memproduksi keempat produk pada mesin 1 adalah 500 jam dan mesin 2 adalah 380 jam. Harga jual per unit keempat produk secara berturut-turut adalah $65, $70, $55 dan $45. Formulasikan permasalahan di atas ke dalam model matematiknya !
Solusi :
Alternatif keputusan adalah : jumlah produk 1,2,3 dan 4 yang dihasilkan.
Tujuannya adalah memaksimumkan keuntungan. Perhatikan, keuntungan diperoleh dengan mengurangkan biaya dari pendapatan.
Keuntungan per unit dari produk 1 = 65 – (10x2 + 3x5) = 30
Keuntungan per unit dari produk 2 = 70 – (10x3 + 2x5) = 30
Keuntungan per unit dari produk 3 = 55 – (10x4 + 1x5) = 10
Keuntungan per unit dari produk 4 = 45 – (10x2 + 2x5) = 15
Sumber daya pembatas adalah waktu kerja yang disediakan kedua mesin.
Definisikan :
x1 : jumlah produk 1 yang dihasilkan
x2 : jumlah produk 2 yang dihasilkan
x3 : jumlah produk 3 yang dihasilkan
x4 : jumlah produk 4 yang dihasilkan
Model umum pemrograman linier :
Maksimumkan z = 30 x1 + 30x2 + 10 x3 + 15 x4
Kendala :
2x1 + 3 x2 + 4x3 + 2x4 ≤ 500
3x1 + 2 x2 + x3 + 2x4 ≤ 380
x1, x2, x3 , x4 ≥ 0
- Suatu perusahaan manufaktur menghentikan produksi salah satu produk yang tidak menguntungkan. Penghentian ini menghasilkan kapasitas produksi yang menganggur (berlebih). Kelebihan kapasitas produksi ini oleh manajemen sedang dipertimbangkan untuk dialokasikan ke salah satu atau ke semua produk yang dihasilkan (produk 1,2 dan 3). Kapasitas yang tersedia pada mesin yang mungkin akan membatasi output diringkaskan pada table berikut :
Tipe mesin | Waktu yang dibutuhkan produk pada masing-masing mesin (jam) | Waktu yang tersedia (jam per minggu) |
Produk 1 | Produk 2 | Produk 3 |
Mesin milling | 9 | 3 | 5 | 500 |
Lathe | 5 | 4 | 0 | 350 |
Grinder | 3 | 0 | 2 | 150 |
Bagian penjualan mengindikasikan bahwa penjualan potensial untuk produk 1 dan 2 tidak akan melebihi laju produksi maksimum dan penjualan potensial untuk produk 3 adalah 20 unit per minggu. Keuntungan per unit masing-masing produk secara berturut-turut adalah $50, $20 dan $25.
Formulasikan permasalahan diatas kedalam model matematik !
Solusi :
Alternatif keputusan :
Jumlah produk 1 yang dihasilkan = x1
Jumlah produk 2 yang dihasilkan = x2
Jumlah produk 3 yang dihasilkan = x3
Tujuannya adalah : memaksimumkan keuntungan
Sumber daya pembatas adalah :
Jam kerja mesin milling per minggu : 500 jam
Jam kerja mesin llathe per minggu : 350 jam
Jam kerja mesin grinder per minggu : 150 jam.
Model matematikanya adalah :
Maksimumkan z = 50 x1 + 20 x2 + 25 x3
Kendala :
9x1 + 3 x2 + 5x3 ≤ 500
5x1 + 4 x2 ≤ 350
3x1 + 2x3 ≤ 150
x3 ≤ 20
x1, x2, x3 g ≥ 0
------------****------------
Siringoringo, Hotniar. Seri Teknik Riset Operasional. Pemrograman Linear. Penerbit Graha Ilmu. Yogyakarta. 2005.

 ,
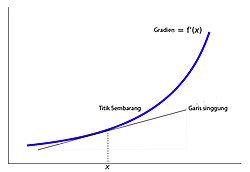
, pada definisi turunan di atas merupakan gradien dari garis sekan yang melewati titik (x,ƒ(x)) dan (x+h,ƒ(x)) pada kurva ƒ(x). Apabila kita mengambil limit h mendekati 0, maka kita akan mendapatkan kemiringan dari garis singgung yang menyinggung kurva ƒ(x) pada titik x. Hal ini berarti pula garis singgung suatu kurva merupakan limit dari garis sekan, demikian pulanya turunan dari suatu fungsi ƒ(x) merupakan gradien dari fungsi tersebut.
pada definisi turunan di atas merupakan gradien dari garis sekan yang melewati titik (x,ƒ(x)) dan (x+h,ƒ(x)) pada kurva ƒ(x). Apabila kita mengambil limit h mendekati 0, maka kita akan mendapatkan kemiringan dari garis singgung yang menyinggung kurva ƒ(x) pada titik x. Hal ini berarti pula garis singgung suatu kurva merupakan limit dari garis sekan, demikian pulanya turunan dari suatu fungsi ƒ(x) merupakan gradien dari fungsi tersebut.